It’s been a sunny day, and after been out with my family, walking a lot and played with my daughter until she’s getting very tired, finally I’m here ready to write a simple post I was thinking about from a while.
Generally speaking, in my work I returned to write tons of code and despite my work is related to the cloud world (openstack, k8s and such of those amazing things), made of abstractions of any type and where the code you write will manipulate very high level data, I found myself nostalgic remembering with a smile the time in which code would be optimized, would have written in resource limited environments and each problem come to a resolution through a process in which software design, algorithms and data structures were involved in a massive way.
Starting from this point, I just thought to start a series of posts related to data structures and algorithms, hoping that I can succeeded in find the time to make this post the p->head of a real series and not an isolated episode. From Java to Golang developers passing through bash (or any kind of) people who like scripts, one of the most popular data structure that come to my mind is the Hashtable and, indeed, it comes with a great story to tell.
The thing made me like: “wow” is that this DS has many apparent authors, but I like to think that was Peter Luhn the first creator, writing the IBM memorandum using hashing with chaining.
And Now, since this is not an historical point of view of this theme, let’s start to talk about how technically it works:

WHAT IS HASHTABLE

As we saw with binary search, certain data structures such as a binary search tree can help improve the efficiency of searches. From linear search to binary search, we improved our search efficiency from O(n) to O(logn) . Now we present a new data structure, called a HashTable, that will increase our efficiency to O(1) , or constant time.

A hash table is made up of two parts: an array (the actual table where the data to be searched is stored) and a mapping function, known as a hash function. The hash function is a mapping from the input space to the integer space that defines the indexes of the array. In other words, the hash function provides a way for assigning numbers to the input data such that the data can then be stored at the array index corresponding to the assigned number.

Let’s take a simple example. First, we start with a hash table array of strings (we’ll use strings as the data being stored and searched in this example).

Let’s say the hash table size is 12:

	[X -X -X -X ..... ]

Next we need a hash function. There are many possible ways to construct a hash function. Let’s assume a simple hash function that takes a string as input and return as hash value the sum of the ASCII characters that make up the string mod the size of the table:

int hash(char *str, int table_size){
	int sum;

	/* Make sure a valid string passed in */
	if (str==X) return -1;

	/* Sum up all the characters in the string */
	for( ; *str; str++) sum += *str;

	/* Return the sum mod the table size */
	return sum % table_size;
}

Now that we have a framework in place, let’s try using it. First, let’s store a string into the table: “Steve”. We run “Steve” through the hash function, and find that hash(“Steve”,12) yields 3:

[X - X - X - "Steve" - X .........]

Let’s try another string: “Spark”. We run the string through the hash function and find that hash(“Spark”,12) yields 6. Fine. We insert it into the hash table:

[X - X - X - "Steve" - X - X - "Spark" .........]

Let’s try another: “Notes”. We run “Notes” through the hash function and find that hash(“Notes”,12) is 3….. Ok…. We insert it into the hash table:

[X - X - X - "Steve","Notes" - X - X - "Spark" ...]   => GENERATE A COLLISION!!

What happened? A hash function doesn’t guarantee that every input will map to a different output (in fact it shouldn’t do this). There is always the chance that two inputs will hash to the same output. This indicates that both elements should be inserted at the same place in the array, and this is impossible. This phenomenon is known as a collision.

There are many algorithms for dealing with collisions, such as linear probing and separate chaining.

While each of the methods has its advantages, we will only discuss separate chaining here.

Separate chaining requires a slight modification to the data structure. Instead of storing the data elements right into the array, they are stored in linked lists. Each slot in the array then points to one of these linked lists. When an element hashes to a value, it is added to the linked list at that index in the array.

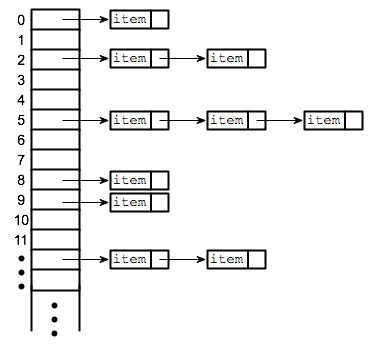
Because a linked list has no limit on length, collisions are no longer a problem. If more than one element hashes to the same value, then both are stored in that linked list.

Let’s look at the above example again, this time with our modified data structure:

[[X],[X],[X],[X],[X],[X],[X],[X],[X],[X],[X],[X],[X]]

Again, let’s try adding “Steve” which hashes to 3, and then “Spark which hashes to 6”:

[[X],[X],[X],["Steve"],[X],[X],["Spark"],[X],[X],[X],[X],[X],[X]]

Now we add “Notes” which hashes to 3, just like “Steve”:

[[X],[X],[X],["Steve","Notes"],[X],[X],["Spark"],[X],[X],[X],[X],[X],[X]]

Once we have our hash table populated, a search follows the same steps as doing an insertion. We hash the data we’re searching for, go to that place in the array, look down the list originating from that location, and see if what we’re looking for is in the list. The number of steps is O(1) .

Separate chaining allows us to solve the problem of collision in a simple yet powerful manner. Of course, there are some drawbacks. Imagine the worst case scenario where through some fluke of bad luck and bad programming, every data element hashed to the same value. In that case, to do a lookup, we’d really be doing a straight linear search on a linked list, which means that our search operation is back to being O(n) . The worst case search time for a hash table is O(n) . However, the probability of that happening is so small that, while the worst case search time is O(n) , both the best and average cases are O(1).

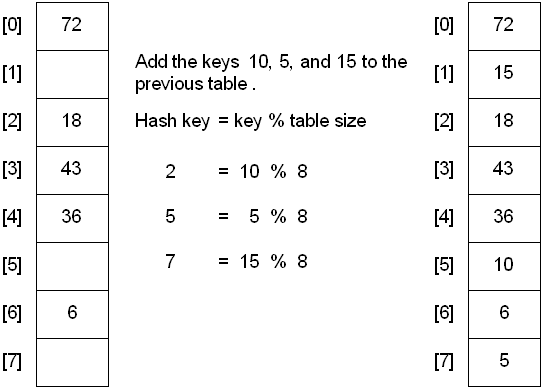
Linear probing is also another technique used to face this kind of problem and it follows this rule: after performing the hash function, if the resulting slot is not availble the item will be stored in the next available slot in the table, assuming that the table is not already full.

Hash Tables With Linear Probing — algs4.cs.princeton.edu

This is implemented via a linear search for an empty slot, from the point of collision.
If the physical end of table is reached during the linear search, the search will wrap around to the beginning of the table and continue from there: if an empty slot is not found before reaching the point of collision, the table is full.
A problem with linear probing is the generation of Primary Clustering, so any key that hashes into the cluster will require several attempts to resolve the collision. There are several algorithms that have tried to solve the primary clustering problem: the first one is the Hashing with Quadratic Probe.
With quadratic probing, rather than always moving one spot, the idea is to make a n^2 steps from the point of collision, where “n” is the number of attempts to resolve the collision. At first glance it seems good, but if the table is more than half full, looking for an empty block become very difficult: this new problem is known as Secondary clustering because elements that hash to the same hash key will ALWAYS proble the same alternative cells. Many attemps are born to try to solve the secondary clustering problem, for example the Hashing with Double Hashing that tries to make the hash section smarter.

Roughly speaking, after executing the first hash if a collision is found a second hash function is applied in order to get an empty block; a popular second hash function is:

        Hash2(key) = R - ( key % R )

where R is a prime number that is smaller than the size of the table.

CONCLUSION

Combining the Double hashing solution with the separate chaining is the best solution and, even if talking about performance is out of the scope of the analysis made in this post, I think it could represent the fair solution.